從科學的角度看聲音

在上一段的教學中，我們使用合成器處理了五個頻率分別為中央Ｃ（261.62赫茲）的整數倍數的振盪器，其結果聽起來仍然是一個單音的（Monophonic）音效。我們知道中央Ｃ的頻率乘上二會產生高八度的Ｃ，乘上四則是高十六度的Ｃ，但它的三倍（785赫茲）和五倍（1308赫茲）一個是Ｇ音，一個是Ｅ音，照理說輸出結果應該是一個多音的（Polyphonic）和弦，實際上在我們耳中，它卻仍然像一個明顯的Ｃ音，為什麼呢？在繼續深究AudioKit之前，讓我先來說說聲音的基本原理。

這個單元中沒有任何的程式碼，如果對於理論沒有興趣，請自行跳過。

若你曾經是，或現在正是理工科的大學生，或許在課程中學到過大多數人談之色變的「傅立葉分析」：任何週期性的波動（Periodic Wave）都可以視為一系列波長成調和級數的正弦波的疊加。我們知道波長和頻率互為倒數，因此波長成調和級數的意思，實際上就是頻率成遞增的自然數比例，因此傅立葉分析正是在說我們剛剛撰寫的合成器播放的Ｃ音，可以視為五個振盪器的疊加，但知道這個道理已經被科學家證明了，又有什麼意義呢？這個問題要從音樂的根本說起。

音樂是什麼？

身為一個蘋果的忠實追隨者，容我用一張 Garage Band 的截圖來回答這個問題，當然，科學家或許也會這麼回答：

而音樂家的回答，或許更貼近一般人的認知...

從更微觀的角度來回答問題，我們可以回想在介紹振盪器時，曾經給大家展示過的正弦波圖：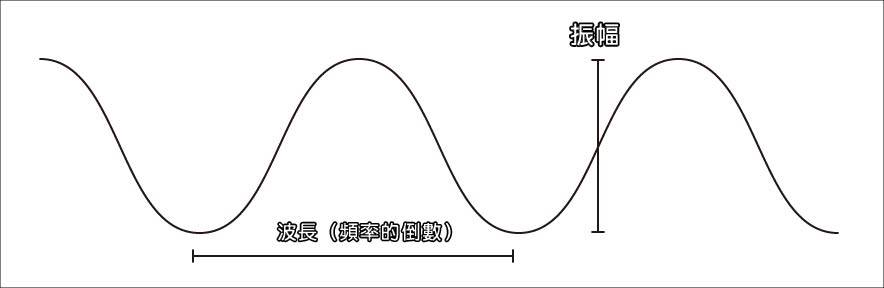

...實際上可以更簡單地用一張圖表達：

在實務上以樂器彈奏時，因為能量守恆定律，振幅會漸漸變小直到消失，所以也不能完全說這個整齊的正弦波與這個音符相等，但只要明白意思就好。

我們所有看到、聽到、摸到的訊息，都具有波動的特性，以現代科學的角度來分析這些訊息時，其實世間的一切不過都像是 Garage Band 中的音訊圖這樣的震動，從這個視角來解釋事件的行為，稱為「時域分析」，即是以時間為基礎，觀察萬物隨著時間不停地改變。而把規律的波動化整為零，以一個音符、一張照片、一縷對雨滴的感嘆來解釋波動，人類使這些抽象的波動有了意義，這個視角叫做「頻域分析」，我們無時無刻不在利用頻域解析萬物，只是沒有自覺而已。

傳說中的傅立葉分析，就是貫穿時域和頻域的鑰匙，它指出任何規則的波動都可以分解為一系列正弦波，關於其詳細原理與科學領域的應用，在此礙於篇幅將不贅述，有興趣的同學可以參考這篇寫的非常棒的文章。我們只直接指出它在音樂上的意義：所有帶有某個音高的規律音調，都可以視為一系列「正弦音調」的混音。這些正弦音調中頻率最低的一組，就是上一段教學中介紹的「基頻」，是區別音高的主要元素，它的同伴們則稱為「泛音」，不同的泛音組合決定了樂器或人聲的音色，而頻率不是整數倍的音調，則稱為不和諧波或「分音音調」，在特定的組合下（例如 C Major 的三個基礎音：Ｃ、Ｅ、Ｇ），分音音調可以構成「和弦」，製造和諧的、且不限於單音調的音樂效果，但無規律的分音音調（例如400、666、987赫茲的搭配）的數量超越某個程度後，就只能組合出「噪音」了。