解析電子音效的「形狀」

聽完了偉大的傅立葉對音效的見解，或許大家的大腦裡仍然是一片混沌：「好吧，現在我們知道了正弦波堆疊、基頻、泛音這些聽起來好像很厲害的名詞，但是到底要幹嘛？」

這個單元中我們再次回到程式碼的世界，認識一個新的AudioKit元件AKPlaygroundView。從它的名字就能大概的猜測出此元件的用途：這是一個相當簡易的class，繼承自UIView，內含幾個方便的指令能幫助我們快速建構一個圖形化的UI介面，例如addLabel指令可快速建立一個文字顯示，利用此元件，我們可以實時的監測關於音效的數據，如頻率、振幅等等。

import AudioKit
import PlaygroundSupport

let oscillator = AKOscillator()
oscillator.frequency = 261.62
oscillator.start()

AudioKit.output = oscillator
AudioKit.start()

// 新增一個AKPlaygroundView，並顯示振盪器的頻率
class PlaygroundView: AKPlaygroundView {
    override func setup() {
        addTitle("Hello World")
        addLabel( String(format:"Freq: %.2f", oscillator.frequency) )
    }
}

PlaygroundPage.current.needsIndefiniteExecution = true
PlaygroundPage.current.liveView = PlaygroundView()

關於PlaygroundPage的介紹可以參照第四週的課程，在此我們設定了一個新屬性needsIndefiniteExecution為true，其效果為讓Playground的模擬器會無止盡的運行，直到我們按下停止鍵為止。我們新增的程式碼功能相當簡單：顯示一個標題，並加入一個標籤，顯示我們使用的振盪器的頻率。

當然，雖然擁有一個圖形化介面很不錯，但目前簡易的顯示功能，對我們理解一個合成音效背後的原理幫助不大，因此我們還需要AKOutputWaveformPlot元件，此元件提供一個非常簡單的介面：createView，此介面回傳一個UIView，我們將上面程式碼的addLabel指令移除，改為加入這個指令，執行看看這個UIView到底是何方神聖。

addSubview(AKOutputWaveformPlot.createView())

AKOutputWaveformPlot的功能就是這麼簡單、暴力而強大：顯示最後AudioKit框架播放的聲音波形，擁有了這個視覺化的聲音「形狀」後，我們再複習一下上一個單元最後提到的定義：頻率最低、波長最長的「基頻」決定了一個聲音的音高，而頻率是基頻整數倍的「泛音」決定了音色，為什麼呢？讓我們更改程式碼，再次使用之前曾經用過的AKMixer製造一個合成音效：

let oscillator2 = AKOscillator()
oscillator2.frequency = 523.24
oscillator2.amplitude = 0.5 // 可自行調整第二個振盪器的振幅，此處我們使用0.5
oscillator2.start()

let mixer = AKMixer()
mixer.connect(oscillator)
mixer.connect(oscillator2)

AudioKit.output = mixer

你輸出的波形可能會和我的不太一樣，AKOutputWaveformPlot使用的是CALayer進行繪製，預設的視圖大小是寬440、高200，而這個合成音的波形將超出繪製範圍，我在這邊手動調整了CALayer的縮放比例，讓我們解釋起來比較方便。

此音波的起始點在A點前的上升路徑正中間，到達A點時，第二個振盪器抵達波峰，此時第一個振盪器正在上升過程中，兩相疊加，造就了最大的振幅，在B點時，第二個振盪器降到了波谷，但第一個振盪器剛剛越過波峰，才剛開始它較緩的一段下降過程，隨後在C點第二個振盪器再次回到波峰，此時第一個振盪器仍在繼續下降，在C點與D點的路徑中間，第一個振盪器終於下到了波谷，此時第二個振盪器下降到一半，之後在D點，第二個振盪器再次抵達波谷，此時第一個振盪器剛開始緩緩上升，造就了另一個最大振幅。

我們將發現，這個波形仍然是一個規律波，它完整的一次波動週期由A-B-C-D-A構成，在這段過程中第一個振盪器恰好也完成一個週期（第二個振盪器則經歷了兩個週期），很明顯的：這個合成波同樣擁有261.62赫茲的頻率，且在一個循環中，僅有一對明顯的波峰和波谷，因此它同樣發出中央Ｃ的音高，只是B、C這一對較小的波峰、波谷改變了它的形狀，因此音色聽起來和單振盪器塑成的正弦波Ｃ音略有不同罷了。

試著調節兩個振盪器的振幅，將第一個振盪器oscillator的振幅降低，第二個振盪器oscillator2的振幅提高，觀察波形的變化：A、D兩個點的振幅將更接近B、C兩個點，雖然此時他仍擁有261.62赫茲的頻率，但我們的人耳在這兩組波峰、波谷的振幅非常接近時，將無法分辨細微的差異，而以為它其實是頻率為523.24赫茲的音高！

下面的另一個實驗中，我們不更改振幅，而是將第二個振盪器改動，分別讓其以659赫茲的頻率和600赫茲的頻率振動，第一個振盪器則維持不變：

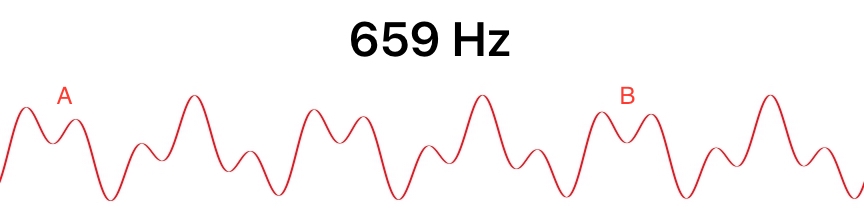
乍看之下，這好像仍然是一個規律波，但仔細比較A點與B點的差異，就能發現它們的形狀有差異，因為659赫茲（接近Ｅ音）並不是261.62赫茲的整數倍，因此這個合成音聽起來就完全不像Ｃ音了，實際上，這是 C Major 和絃的下半部分。

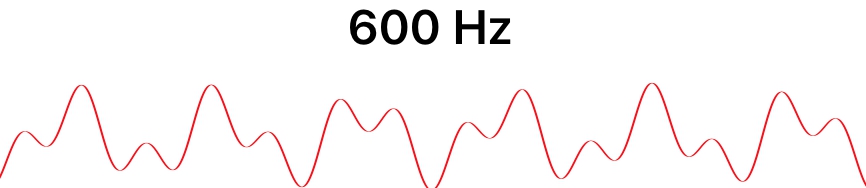
600赫茲並不接近任何絕對音階上的音色（它位於Ｄ音和Ｅ音中間，比較接近Ｄ音），從它的波形上更容易看出不規律性，大量混合這種毫不相干的正弦波，很容易就能產生一個噪音了。